Андрей Андреевич Болибрух - Проблемы Гильберта (100 лет спустя)
 | Название: | Проблемы Гильберта (100 лет спустя) |
Автор: | Андрей Андреевич Болибрух | |
Жанр: | Детская образовательная литература, Математика | |
Изадано в серии: | неизвестно | |
Издательство: | Издательство Московского центра непрерывного математического образования | |
Год издания: | 1999 | |
ISBN: | неизвестно | |
Отзывы: | Комментировать | |
Рейтинг: | ||
Поделись книгой с друзьями! Помощь сайту: донат на оплату сервера | ||
Краткое содержание книги "Проблемы Гильберта (100 лет спустя)"
Знаменитые проблемы, сформулированные Давидом Гильбертом на Парижском международном математическом конгрессе 1900-го года, оказали определяющее влияние на развитие математики XX столетия. Одна из целей этой брошюры - показать, что многие известные и достаточно сложные математические проблемы возникают вполне естественным образом, так что даже старшеклассник может понять причины появления этих проблем и их формулировки.
Текст брошюры представляет собой обработку записи лекции, прочитанной автором 23 октября 1999 года на Малом мехмате для школьников 9-11 классов.
Читаем онлайн "Проблемы Гильберта (100 лет спустя)". [Страница - 4]
Есть и другой способ установить это соответствие, например, выписать все целые числа в таблицу, как показано на рисунке, и, обходя её по стрелочкам, присваивать каждому целому числу некоторый номер. Таким образом, мы «пересчитаем» все целые числа: каждому z ∈ Z сопоставляется некоторое натуральное число (номер) и для каждого номера есть такое целое число, которому этот номер приписывается. При этом явную формулу выписывать не обязательно.
![Книгаго, чтение книги «Проблемы Гильберта (100 лет спустя)» [Картинка № 2] Книгаго: Проблемы Гильберта (100 лет спустя). Иллюстрация № 2](/icl/i/14/542114/image002.jpg)
Таким образом, Z эквивалентно N.
Всякое множество, эквивалентное множеству натуральных чисел, называется счётным. Такое множество можно «пересчитать»: пронумеровать все его элементы натуральными числами.
На первый взгляд, рациональных чисел на прямой «намного больше» чем целых. Они расположены всюду плотно: в любом сколь угодно малом интервале их бесконечно много. Но оказывается, что множество Q также счётно. Докажем сначала счётность Q+ (множества всех положительных рациональных чисел).
Выпишем все элементы Q+ в такую таблицу: в первой строке — все числа со знаменателем 1 (т. е. целые), во второй — со знаменателем 2 и т. д. (см. рисунок на с. 11). Каждое положительное рациональное число обязательно встретится в этой таблице, и не однажды (например, число 1 = 1/1 = 2/2 = 3/3 = … встречается в каждой строке этой таблицы ).
- 10 -
А теперь мы пересчитаем эти числа: идя по стрелочкам, присваиваем каждому числу номер (или пропускаем это число, если оно уже встречалось нам раньше в другой записи).
Поскольку мы двигаемся по диагоналям, то мы обойдём всю таблицу (т. е. рано или поздно доберёмся до любого из чисел).
![Книгаго, чтение книги «Проблемы Гильберта (100 лет спустя)» [Картинка № 3] Книгаго: Проблемы Гильберта (100 лет спустя). Иллюстрация № 3](/icl/i/14/542114/image003.jpg)
Итак, мы указали способ пронумеровать все числа из Q+, т. е. доказали, что Q+ счётно.
Заметим, что этот способ нумерации не сохраняет порядка: из двух рациональных чисел большее может встретиться раньше, а может — и позже.
Как же быть с отрицательными рациональными числами и нулём? Так же как с космозоологами и филателистами в бесконечной гостинице. Пронумеруем Q+ не всеми натуральными числами, а только чётными (давая им номера не 1, 2, 3, ..., а 2, 4, 6, ...), нулю присвоим номер 1, а всем отрицательным рациональным числам присвоим (по такой же схеме, что и положительным) нечётные номера, начиная с 3.
Теперь все рациональные числа занумерованы натуральными, следовательно, Q счётно.
Возникает естественный вопрос:
Может быть, все бесконечные множества счётны?
- 11 -
Оказалось, что R — множество всех точек на числовой прямой — несчётно. Этот результат, полученный Кантором в прошлом веке, произвёл очень сильное впечатление на математиков.
Докажем этот факт так же, как это сделал Кантор: с помощью диагонального процесса.
Как мы знаем, каждое действительное число х можно записать в виде десятичной дроби:
х = А, α1 α2 ... αn ...,
где А — целое число, не обязательно положительное, a α1, α2, ... αn, ... — цифры (от 0 до 9). Это представление неоднозначно: например,
1/2 = 0,50000... = 0,49999...
(в одном варианте записи, начиная со второй цифры после запятой, идут одни нули, а в другом — одни девятки). Чтобы запись была однозначной, мы в таких случаях всегда будем выбирать первый вариант. Тогда каждому числу соответствует ровно одна его десятичная запись.
Предположим теперь, что нам удалось пересчитать все действительные числа. Тогда их можно расположить по порядку:
х1 = А, α1 α2 α3 α4 ...
х2 = B, β1 β2 β3 β4 ...
х3 = С, γ1 γ2 γ3 γ4 ...
х4 = D, δ1 δ2 δ3 δ4 ...
………
Чтобы прийти к противоречию, построим такое число у, которое не сосчитано, т. е. не содержится в этой таблице.
Для любой цифры а определим цифру ̅а следующим образом:
![Книгаго, чтение книги «Проблемы Гильберта (100 лет спустя)» [Картинка № 4] Книгаго: Проблемы Гильберта (100 лет спустя). Иллюстрация № 4](/icl/i/14/542114/image004.jpg)
- 12 -
Положим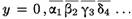
Книги схожие с «Проблемы Гильберта (100 лет спустя)» по жанру, серии, автору или названию:
 |
| Елена Анатольевна Бойко - Лучшие подвижные и логические игры для малышей от 3 до 6 лет Жанр: Детская образовательная литература Год издания: 2008 |
 |
| Ирина Игоревна Бурова, Анатолий Викторович Буров - Программа развития и обучения дошкольника. Английский язык в песенках. Для детей 4-6 лет. |
 |
| Алексей Владимирович Владимиров - Летучие пленники Жанр: Детская образовательная литература Год издания: 1973 |
 |
| Владимир Андреевич Мезенцев - Человек ищет чудо Жанр: Детская образовательная литература Год издания: 1978 |


